Debunking Flat Earth
YouTube Playlists
-
Main Videos
-
Debate Clips
-
“Blind Village” Clips
-
Full Debates
Contents
This information was originally presented in the following clip:
Unlike ancient cultures, modern flat earthers claim the sun never goes below eye level and instead sets by moving away due to perspective. More on this below, under the heading “Rowbothamism.”
This means that their fatal flaw is sunset contrasted against the geometry of perspective. The way that flat earthers try to explain perspective is a mess of nonsense that globers have begun to call “flerfspective.”
The correct geometry for their claim is as follows:
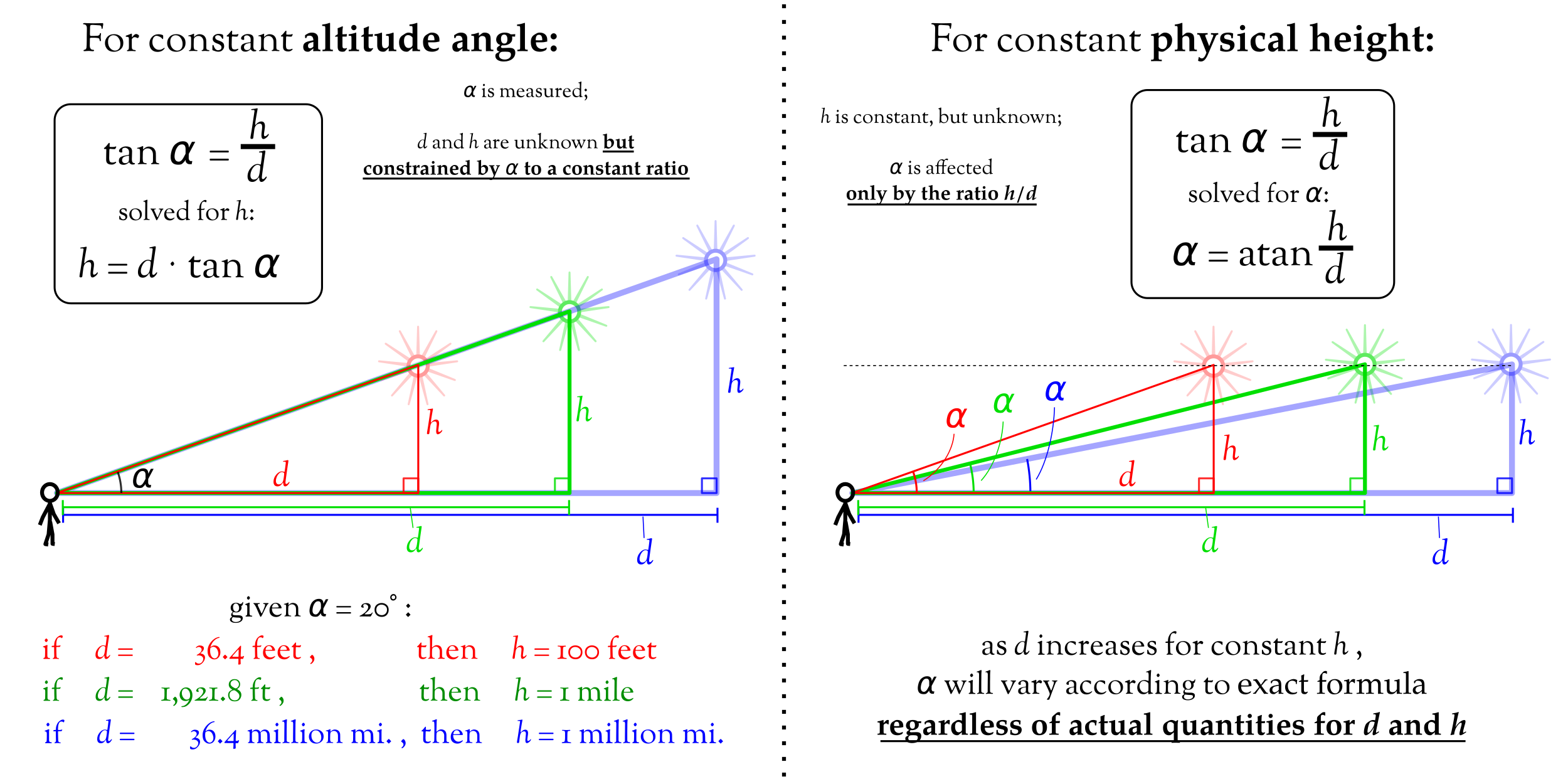
As the right side shows, the angle of a flat earth sun would follow an arctangent function, which is extremely nonlinear. I demonstrated this by holding a flashlight at my waist and walking away from my camera until I disappeared. If we overlay frames from this video at a constant interval, we see extremely variable spacing:

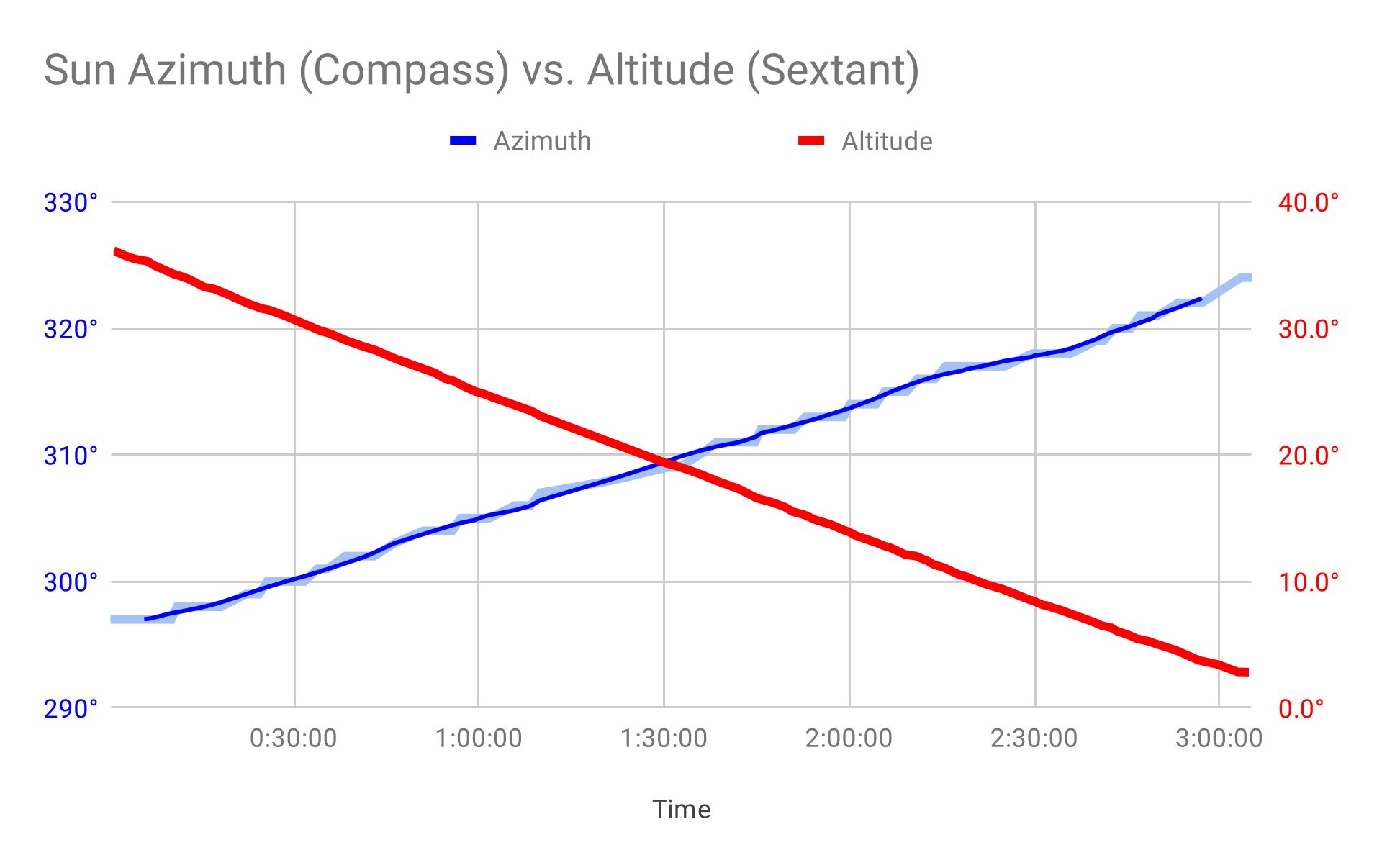
But this is not what we observe with sunset. On May 31, 2019 I went to Hoover Reservoir in Ohio and recorded 3 hours of sunset from 5:35pm to 8:40pm EDT.
I had two identical cameras side by side, one with welding glass over the lens and one without, to help show the vastness of the dynamic range:

For numeric certainty, I also measured the azimuth & altitude of the sun during the entire experiment. To do this, I taped a compass and sextant to a level spinning table:


Here's the full experimental data:
Here, I mimicked the previous composite by overlaying frames at a constant interval, showing fixed spacing. So even at a glance, the Rowbothamist flat earth sun is falsified. The sun sets by going down, not away.

The quantitative data fully confirms this:
 ≠
≠

This information was originally presented in the following clip:
You may have seen the commonly shared flat earth meme on the left. It is sheer misinformation, which I have shown corrected on the right.

Flat earthers claim their view is the “default,” similar to ancient cosmologies; and that belief in a globe is the anomaly. This is a lie, because of one simple question of cosmology: Where does the sun go at night?
Ancient cosmologies generally believed the sun went either below the earth at night, or out of the firmament to somewhere unknown. This means they assumed the whole world experienced one universal time of day or night.
In the age of time zones, modern flat earthers try to resurrect flat earth by saying that at night the sun goes “too far away to see.” This not only separates their model from ancient ones, but also violates basic observational science. It traces back to a 19th-century misfit named Samuel Rowbotham, and for that reason I call it “Rowbothamism.”
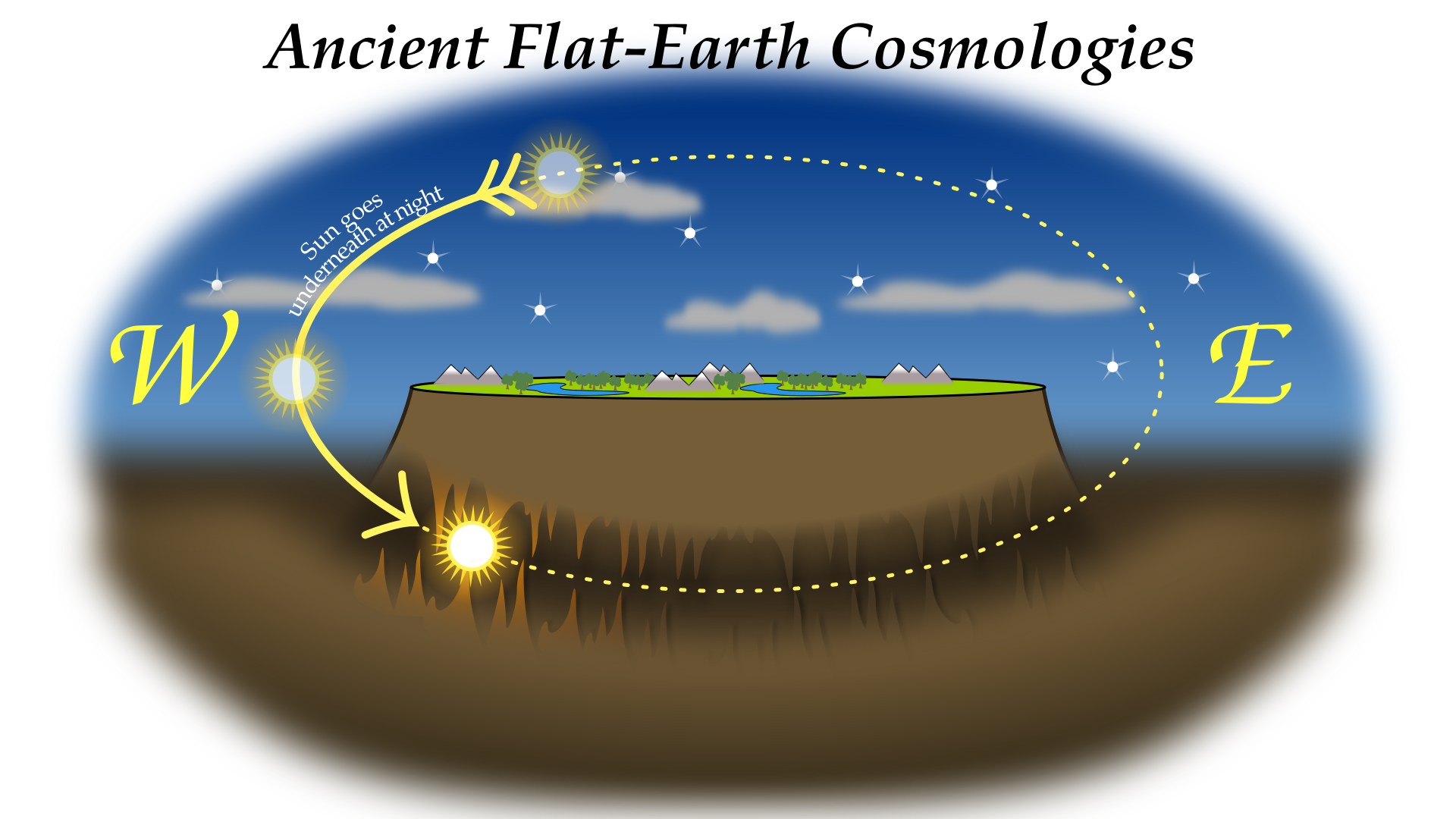

I did my best to survey ancient cultures all over the world. Here is what I found:
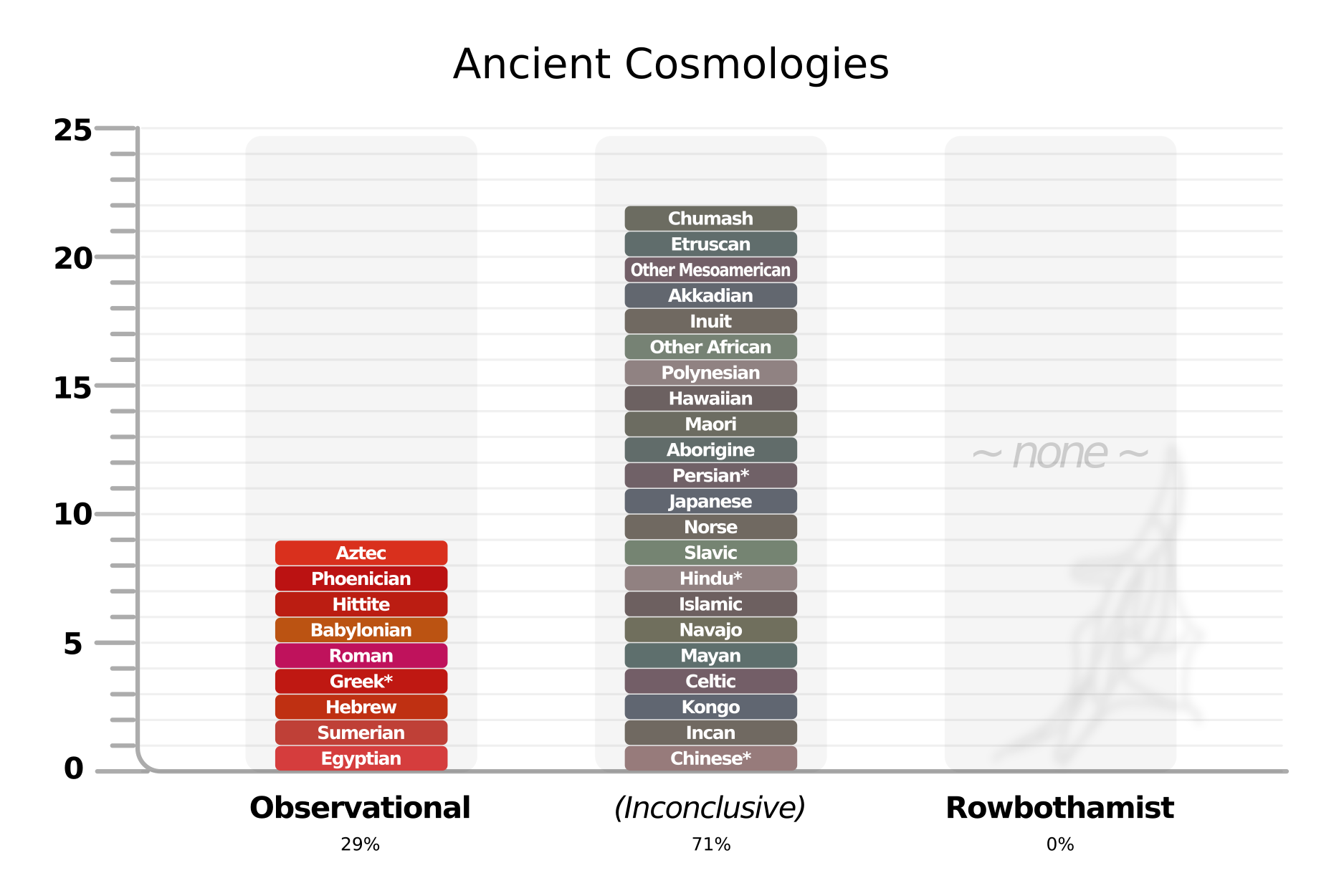
Highlights opposing Rowbothamism
-
Sumerian cosmology
This culture believed there is a tunnel under the earth called the “Road of the Sun.” There's a whole scene in the Epic of Gilgamesh, tablet 9, when Gilgamesh travels along this tunnel to the underworld.
-
Egyptian cosmology
The Egyptian sun god Ra travels in a boat through the underworld every night, and is reborn in the east every morning. This nightly journey was central to Egyptian religious practices, and was described in great detail in the Book of Gates.
-
Aztec cosmology
In Aztec belief, the earth goddess Tlaltecuhtli swallows the sun every evening and vomits it again in the morning.
-
Hebrew cosmology
The Bible does not give any clues about where the sun goes at night, except the use of “rise” and “set” in Matthew 5:45 and Ephesians 4:26. For more detail most sources, including Michael Heiser, look instead to the Book of Enoch.
This 1909 Mormon source summarized the evidence well:
“It was represented that in the eastern side or the face of the firmament there were six doors or portals through which the sun entered from chambers outside the vault, and that in the western side of the firmament there were also six portals. For thirty days the sun passed through the first portal and at evening, after traversing the sky, passed out through the corresponding opening in the west. At the end of the month the sun entered by the second portal; and so on until the sixth had been reached …”
Best scraps supporting Rowbothamism
-
Greek
“[Anaximenes] says that the stars do not move under the earth, as others assume, but round the earth as a cap is turned on one's head, and that the sun is hidden, not because it is under the earth, but because it is hidden by the earth's higher parts, and by reason of its greater distance from us.”
— Hippolytus Refutation of all Heresies; Book I, sec. 6 “Anaximenes”
This idea was highly peculiar: from only one Greek school (Miletus) among many, and apparently idiosyncratic even within that school. Anaximenes' own fellow (and possible teacher) Anaximander imagined the sun moon and stars as holes in giant “chariot wheels” with earth at their center, contradicting Anaximenes' idea. Hyppolytus seems to have found it noteworthy precisely because it was so contrary; and the idea was clearly defeated in general Greek thought by the likes of Pythagoras and others.
-
Chinese
“It is like a person carrying a torch. When he walks away, the light becomes fainter and fainter until it is extinguished. When the sun sets, it is the same.”
— Huainanzi 3.12 (“Patterns of Heaven”)
Chinese cosmology evolved many times over the centuries, and the quote above seems to be a blip on the radar. One of the most classic Chinese myths, “Houyi and the Ten Suns,” strongly suggests that times of sunrise and sunset were considered universal. Other sources say the earth was “bulging up slightly” to account for time differences. More info →
-
Hindu
“The sun, stationed, as it were, in the middle of the day and of the night, enlightens all the regions, whilst its rising, or its setting, is always relative to some portion of space. By this twofold cause, the vicissitudes of day and night ever recur.”
— Vishnu Purana, Book 2, Chapter 8
“When the sun travels from Devadhani, the residence of Indra, to Samyamani, the residence of Yamaraja, it travels thirty-four thousand three hundred yojanas (275,440 miles) in fifteen ghatikas (six hours). Similarly, when it travels from Samyamani to Nimlocani, the residence of Varuna, it travels the same distance in the same amount of time. Then, when it travels from Nimlocani to Vibhavari, the residence of the moon-god, it travels the same distance in the same amount of time. In this way, the sun continues circumambulating Mount Meru.”
— Bhagavata Purana, Canto 5, Chapter 21, verses 7-9
-
Persian
“Of Mount Albûrz it is declared, that around the world and Mount Têrak, which is the middle of the world, the revolution of the sun is like a moat around the world; it turns back in a circuit owing to the enclosure of Mount Albûrz around Têrak. As it is said that it is the Têrak of Albûrz from behind which my sun and moon and stars return again.”
— Pahlavi Texts, Part I, Chapter V, verses 3-4 (SBE05), E.W. West, tr. [1880], at sacred-texts.com
This text, though at first seeming to parallel the Bhagavata Purana above and thus favoring Rowbothamism, goes on to discuss the “apertures” in this uncertain “enclosure of Mount Albûrz” through which the sun enters and exits, now seeming to parallel the Book of Enoch in opposition to Rowbothamism. What this author actually imagined may be more complex than it first appears.
This information is also presented in the following video:
The all-time favorite argument of Rowbothamists, for some reason, uses the worst scientific methodology imaginable. I wonder why?
It's like trying to see outside, but instead of choosing the large clear window nearby, you choose the small dirty one:

Flat earthers present a photograph or video showing some distant object (a mountain, city skyline, etc.), seen in blurry haze across miles of lake or ocean. They also give the “globe prediction,” according to pure geometry, of linear drop from a tangent at the horizon to some part of the visible object (but in far less coherent terms), and boldly declare that it “shouldn't be visible” with curvature. One of their sources tried to tabulate these observations here.
The issues with this argument are almost too many to name, but I will try:
- Their evidence is often obtained through a long chain of memes and other careless (or even dishonest) means, which leads to a plague of misinformation and poverty of data. Errors and missing variables abound; confidence and rigor is an absolutely foreign concept.
- They often neglect observer height, especially if they cite the “8 inches per mile, squared” curvature approximation (which fundamentally excludes observer height).
- They almost never denote the actual height of the target that's visible (unless they think it helps their argument).
- They never coherently address why some part of the target might not be visible. (They give word salad about perspective, opacity, and ocean waves.)
- They give the “missing curvature [drop]” in linear units, which is not coherent for an optical measurement that should be in angular units.
- They try to gatekeep the use of atmospheric refraction as an explanation, despite a source that they cherry-pick clearly describing it as a “nasty complication.”
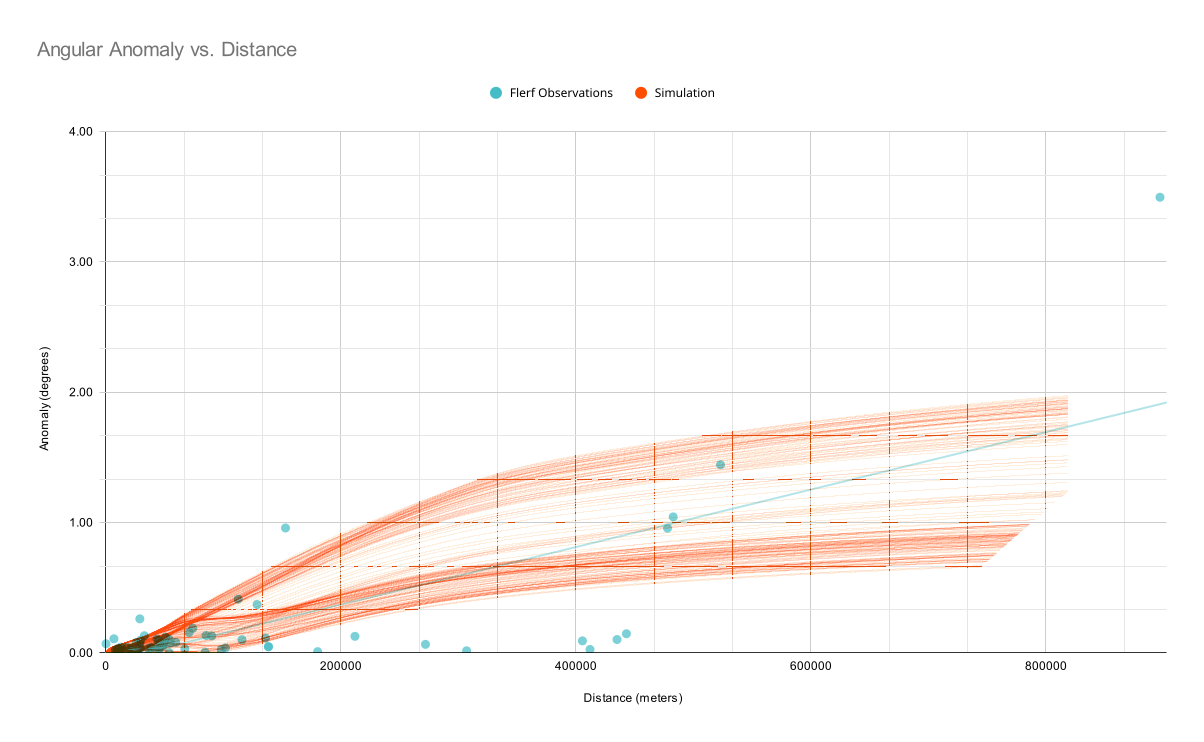
All of these issues boil down to one simple fact: flat earthers are bad at science. They have almost no power of deductive reasoning beyond a brutish intuition. Taking their tabulated data (linked above), even disregarding the virtual certainty of some falsehood in the left hand columns, the data we can cross-check is riddled with errors.
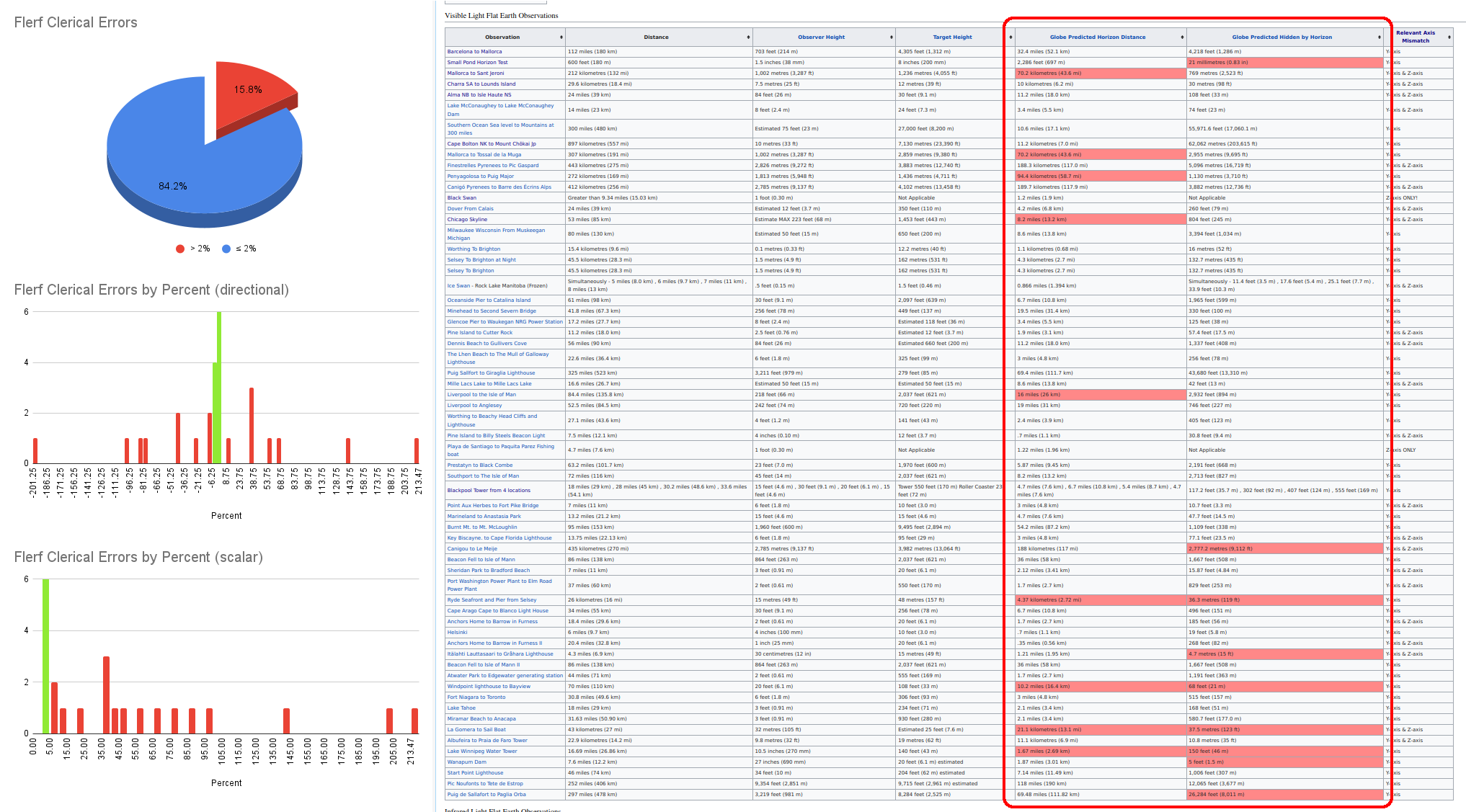
Additionally, when we consider these alleged anomalies as angular displacement in the observer's eye, we find that 94% of them are smaller than a U.S. dime held at arm's length (conservatively speaking).
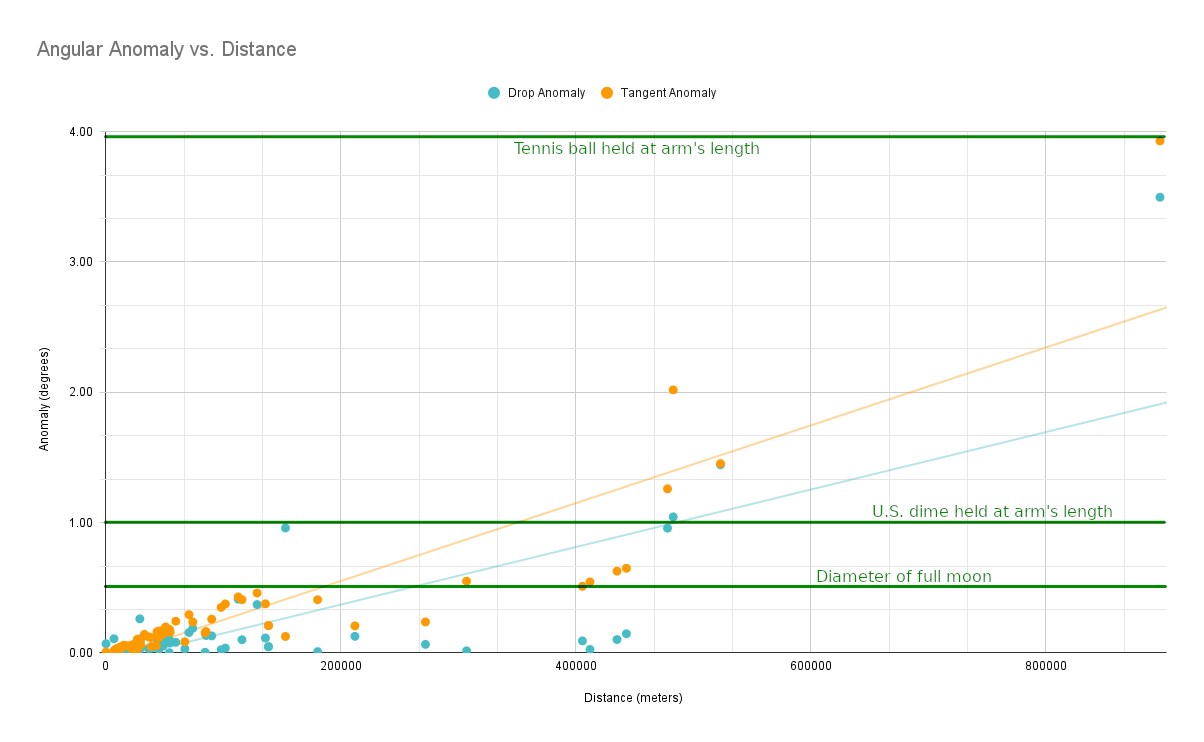
This, along with the 4-degree outlier in the top-right, all makes sense considering the stochastic nature of the weather conditions that drive refraction. There is no true “maximum distance” beyond which it is “impossible” to ever see on the globe; it's simply a matter of the requisite conditions being more and more rare for larger distances. It would require more and more air masses of certain types to perfectly align in a longer and longer refractive corridor around the earth's surface along our line of sight, which is a matter of sheer dynamics.
Notice that flat earthers never perform any measurement or analysis of this refraction whatsoever. Considering its complexity, I hardly blame them for that; but it does completely invalidate their attempt at science.
More info on the graphics above:
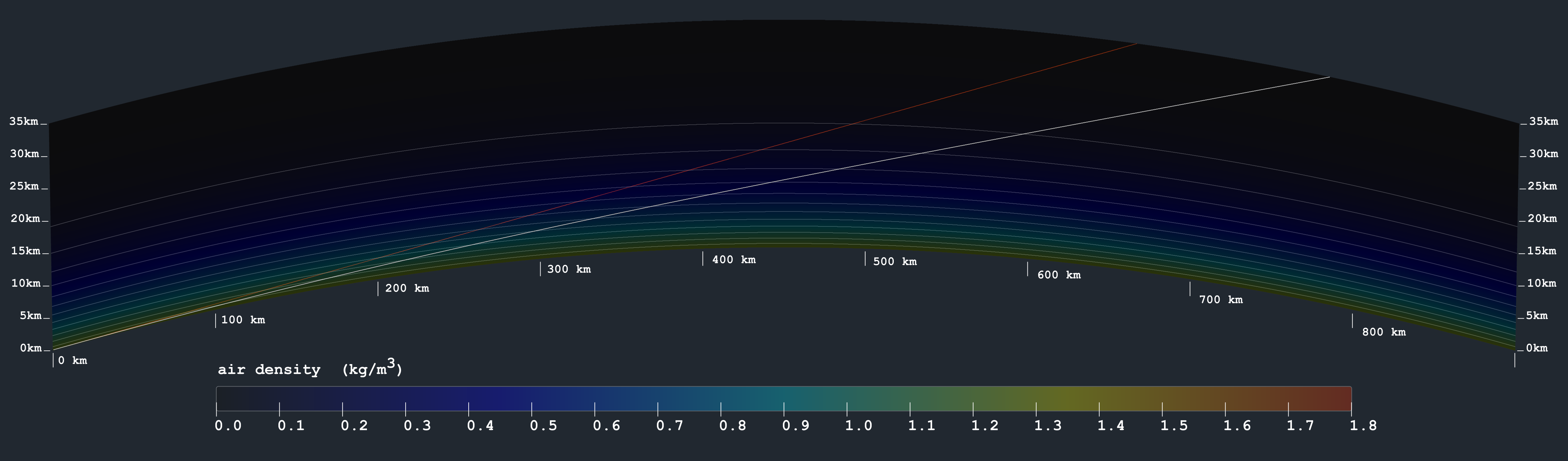
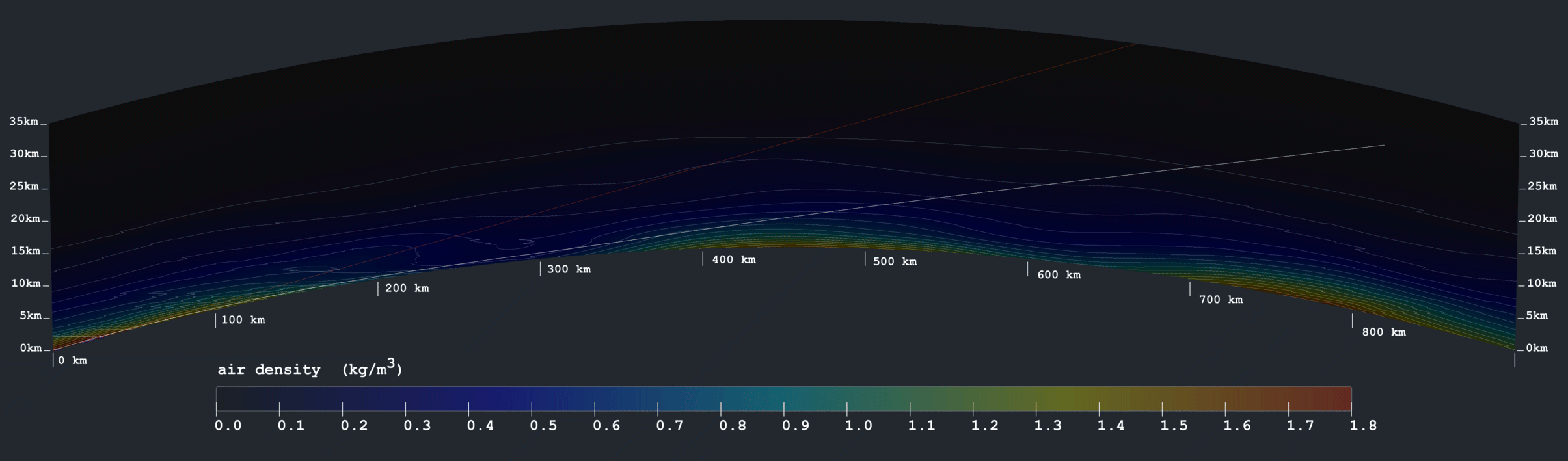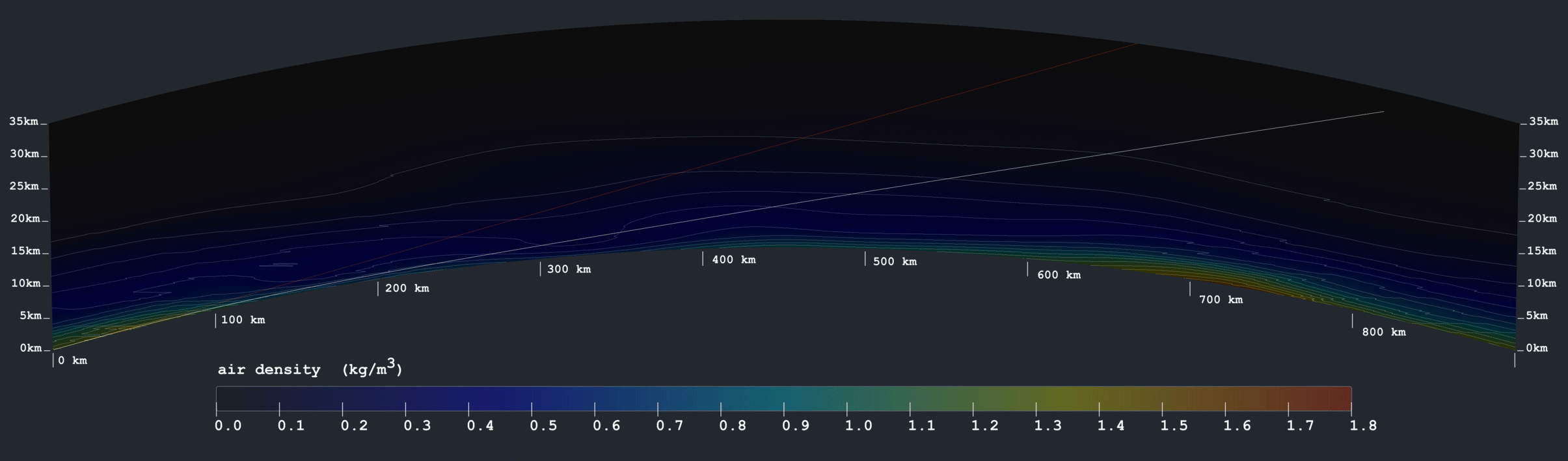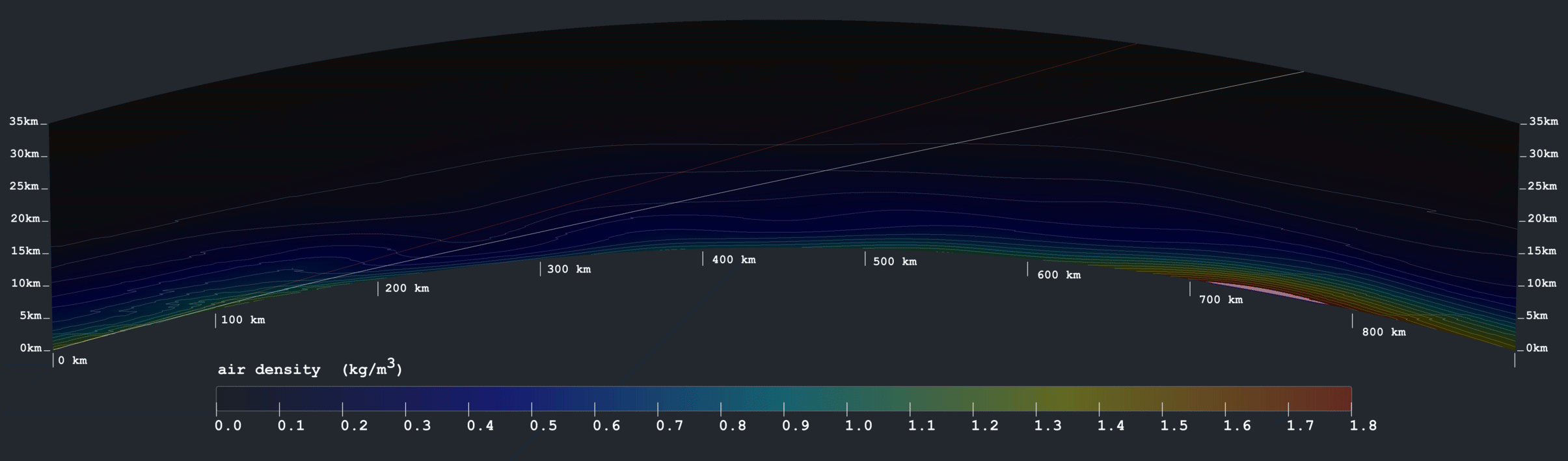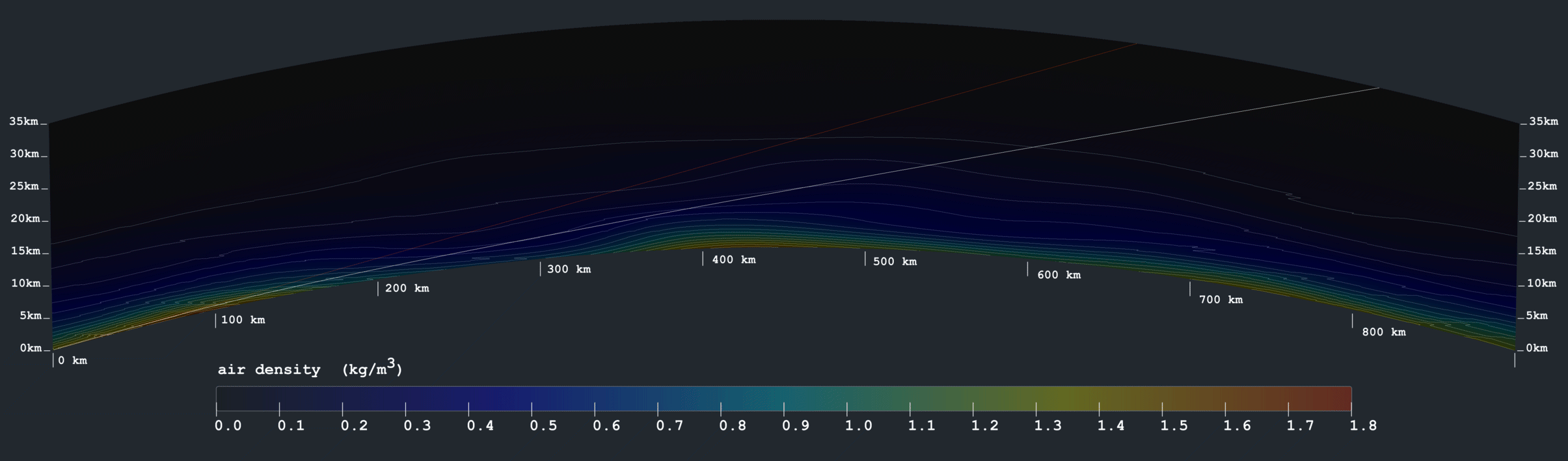
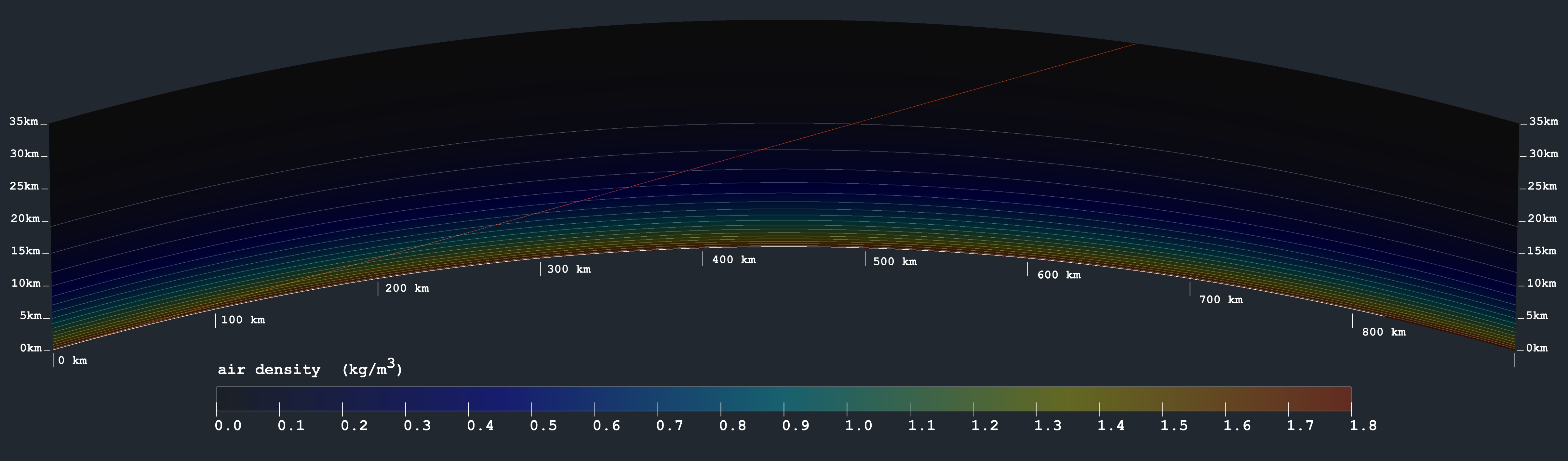
Now, if that were not enough, I wrote a simulation to model atmospheric refraction on a globe. It uses all the most exact, most standard globe and atmosphere metrics, combined with a simple straightforward implementation of Snell's Law:
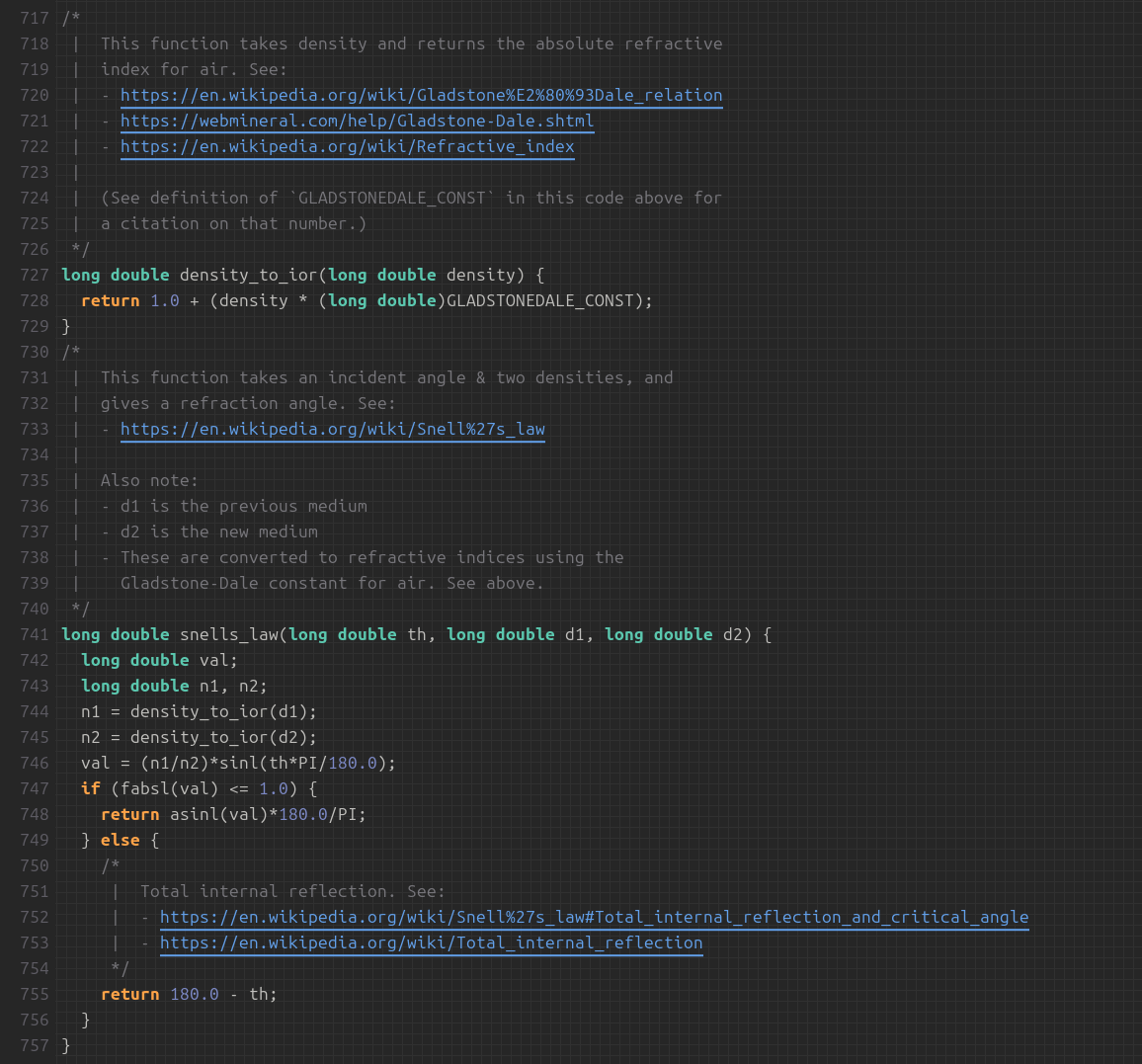
Before any turbulence whatsoever is added, with 100% standard atmospheric gradient, here's how it looks. It renders a vertical cross-section showing density; a straight line in red for reference; and a white line showing continuous deflection due to Snell's Law. The curvature of earth is exaggerated by a factor of 4, just so the diagram will fit on the screen.
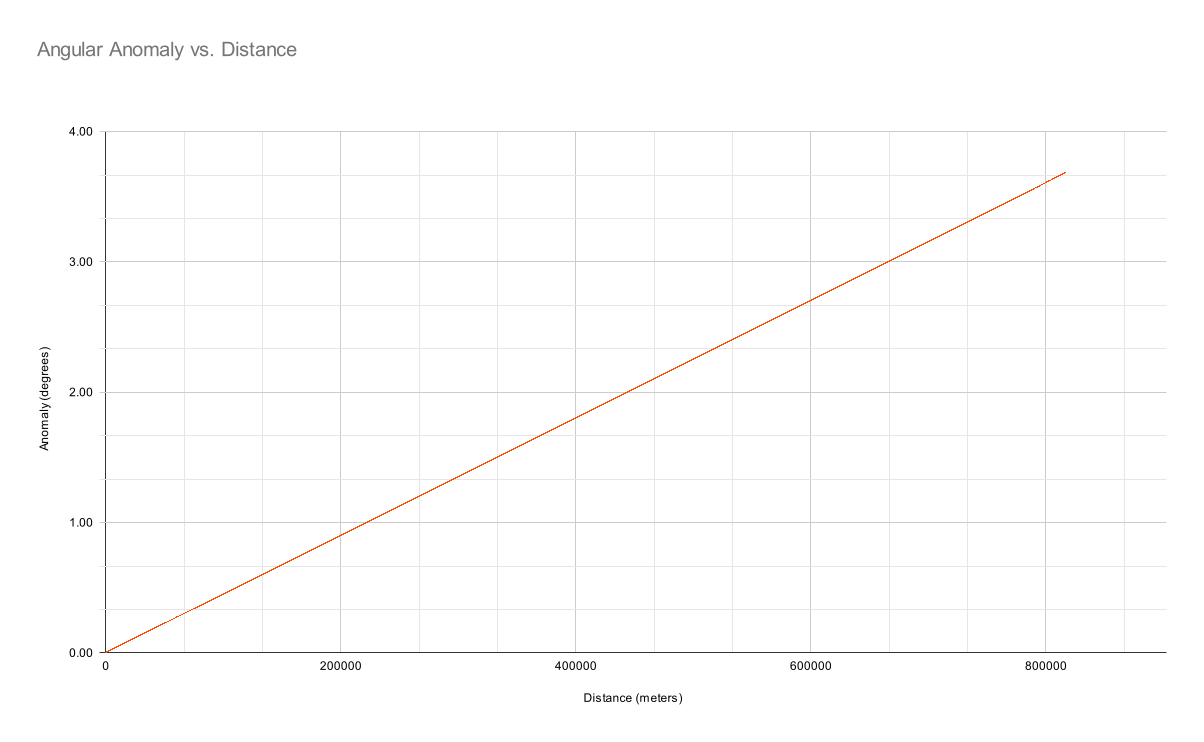
We can also plot this on our previous angular anomaly chart:
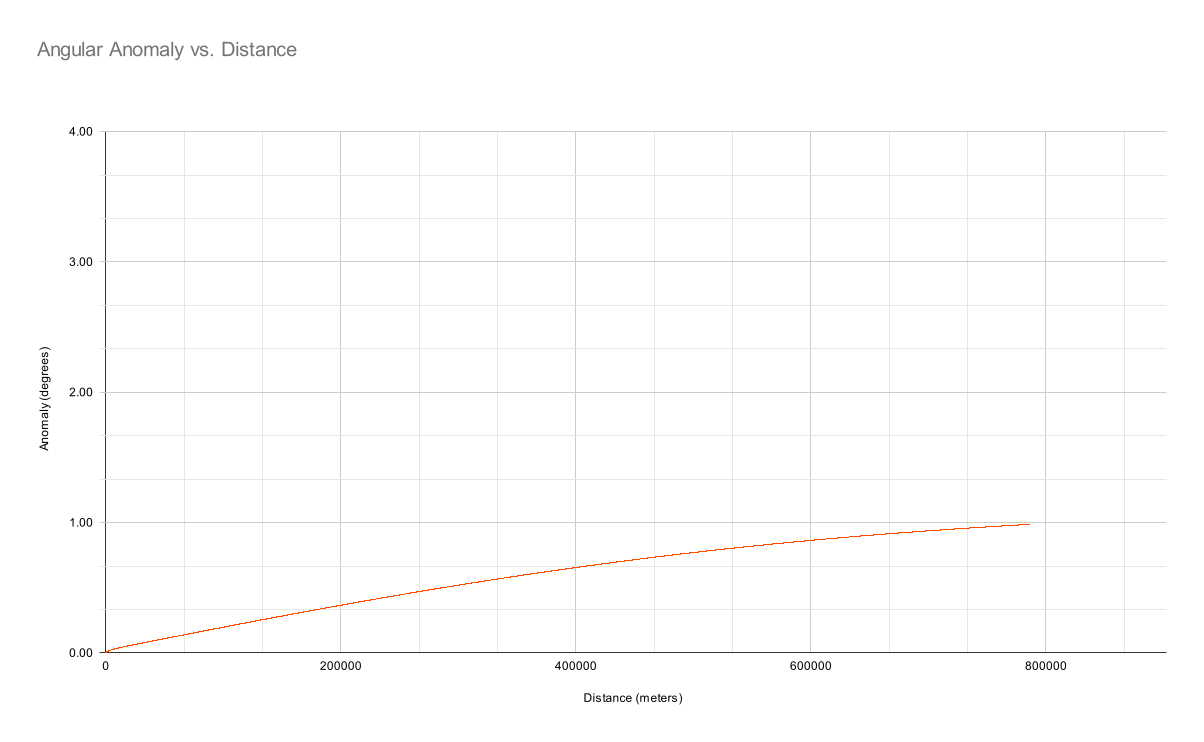
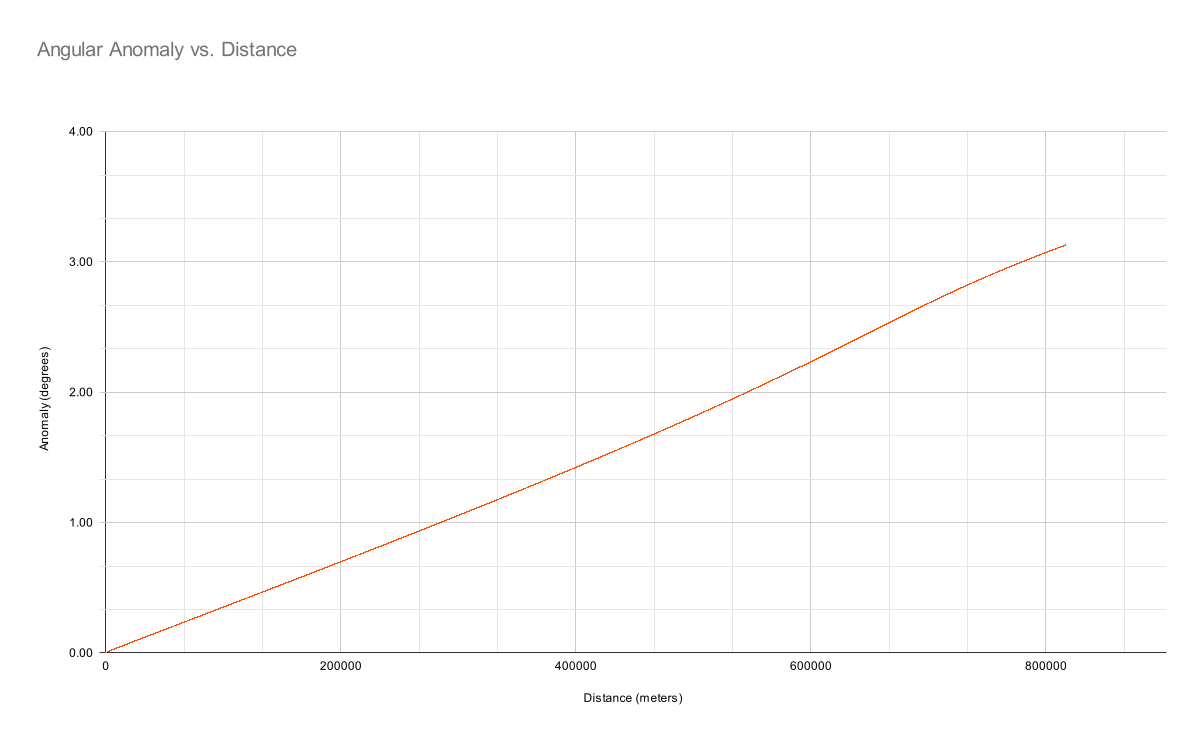
But the atmosphere is far from static. Let's see if we can add some turbulence, lightly chosen to imitate the obvious selection bias in the flat-earthers’ data:
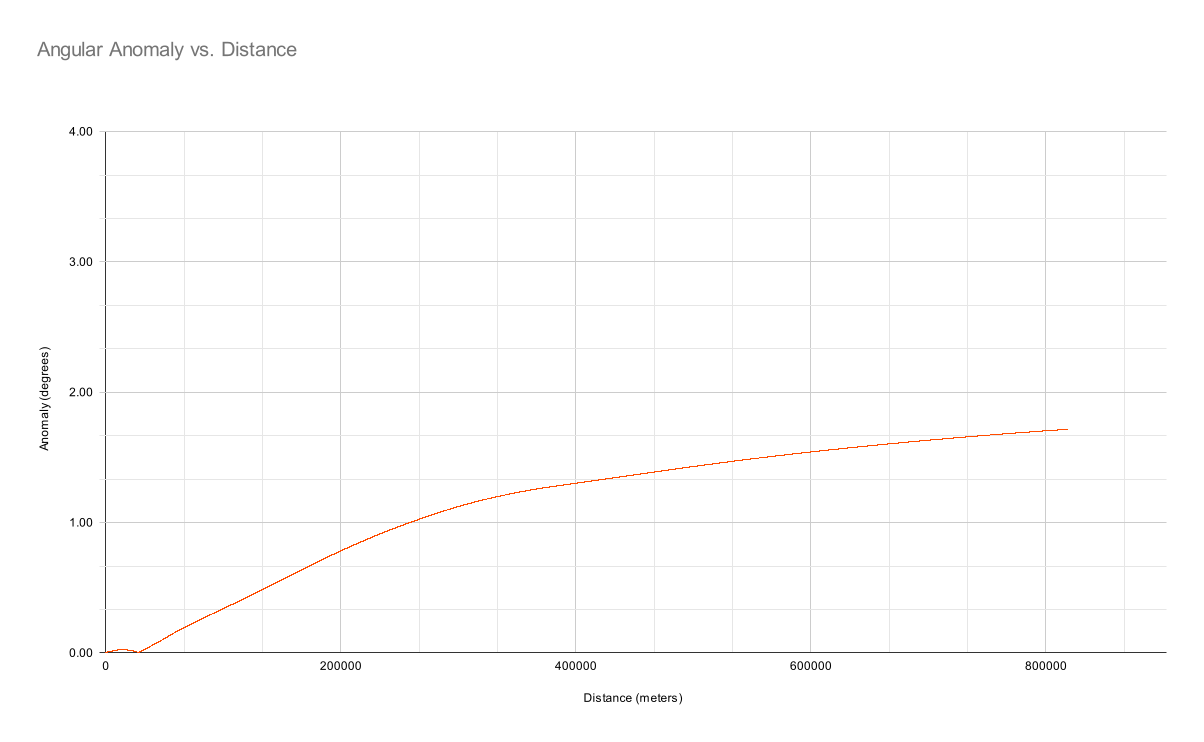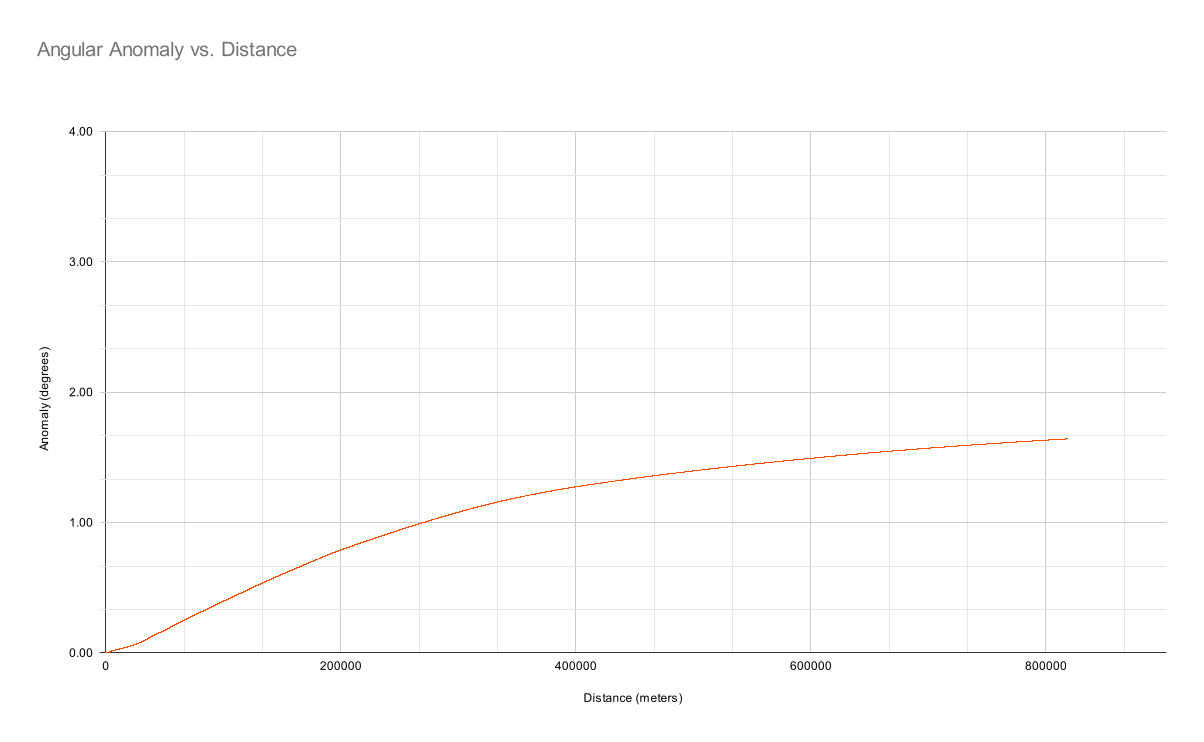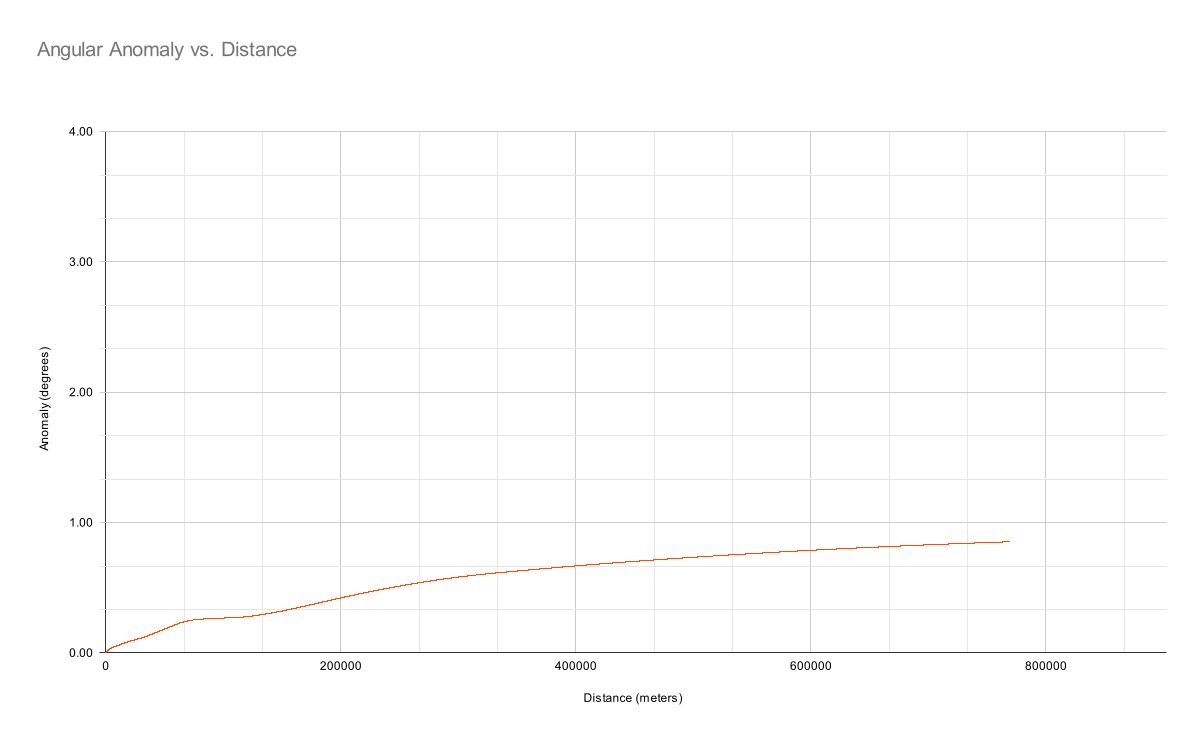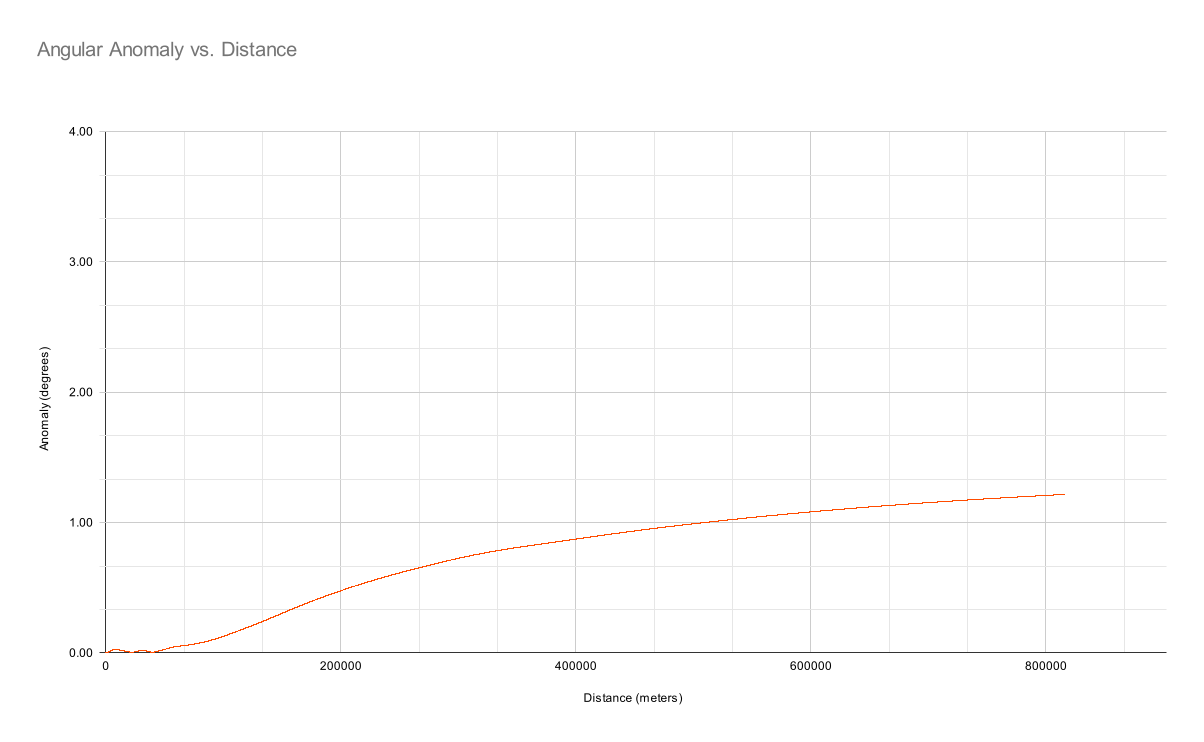
How does that compare with the observation data? Uh-oh …
But that's just random turbulence. The reality is, conditions on clear sunny days, especially over water, create something called a temperature inversion. Others like Michael Toon and Danny Faulkner have provided info on this in more depth, but allow me to connect the dots a little bit.
Here is the Ideal Gas Law:

where:
- p = pressure
- V = volume
- T = temperature
- n = number of molecules (basically)
- R = the ideal gas constant
This form of the gas law is useful when you have a fixed number of gas molecules like in a balloon or a piston chamber, where n is constant and V might be variable; but it's but not so useful for analyzing open portions of the earth's atmosphere. This lack of intuitive applicability is something that flat earthers try to endlessly exploit, while cherry-picking science literature and spewing abject nonsense.
To make the analysis, we have to use the molar form of the gas law, solved for density d:

where M is the air's molar mass. What happened to V? With the introduction of molar mass, we unlocked total mass as a variable which then got combined with volume and became density. We can now treat M/R as a constant, which leaves a fairly simple three-way correlation between density, pressure, and temperature.
But the weird thing is, under standard atmospheric conditions all three of these variables decrease with altitude. How? Because the numerator (pressure p) falls off much faster than the denominator (temperature T), which causes the quotient (density d) to fall too.
Notice what a temperature inversion does to this situation: if the numerator already decreases quickly with altitude, but now the denominator starts actually increasing … then the quotient is going to drop off very, very fast. None of the gradients invert except temperature; and the density gradient becomes extreme.
Let's try to imitate this in the simulation:
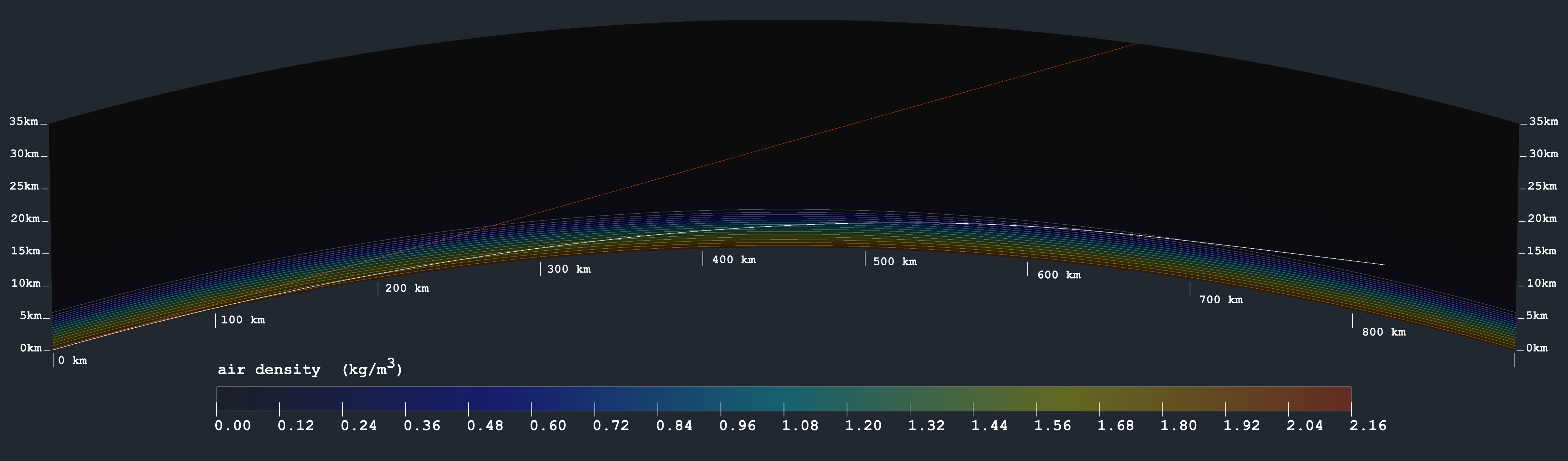
But with a superior mirage involving internal reflection, the gradient doesn't even have to be very extreme:
In conclusion: have flat earthers “falsified the radius value?” No, not even close. The observed data is not only possible, but fully expected given the basic facts about earth, its atmosphere, and simple 11th-grade optics.
Any claim otherwise is sheer ignorance of those topics.
This information is also presented in the following video:
On May 14, 2025, a notorious flat earther named David Weiss (alias DITRH for “Deep Inside The Rabbit Hole”) uploaded a video of himself arguing with ChatGPT about the ISS. I don't normally watch flat earth content, so I saw this through a response video by Bob the Science Guy. Even though Bob's response was excellent, I felt there was something to add.
Here's an excerpt of Dave's argument:
DITRH: Would you say it's fair to compare the size of the International Space Station to a 747? Pretty close, right?
ChatGPT: Yes. The International Space Station is roughly about the size of a 747.
DITRH: Okay. A 747 at cruising altitude of let's say 7 miles. A viewer looking at it with their naked eyes sees a very small airplane in the sky. You agree, right?
ChatGPT: Yes. At about 7 mi high, a 747 looks quite small to the naked eye.
…
DITRH: Let's make it 25 miles high. Could I see it?
ChatGPT: At 25 mi high, a 747 would be practically invisible.
DITRH: How about 50 mi high? Could I see it?
ChatGPT: At 50 mi high, a 747 would be completely invisible to the naked eye.
DITRH: What if the 747 was very reflective and the sun was reflecting off the bottom of it right towards me? Would I be able to see it at at 25 miles high?
ChatGPT: Even if the 747 were very reflective, at 25 m high, it would still be extremely difficult to see with the naked eye.
DITRH: What if it was 100 miles high? Would I be able to see it?
ChatGPT: At 100 miles high, a 747 would be completely invisible to the naked eye regardless of reflectivity.
…
DITRH: So the ISS when it's directly over me is 250 mi away at its very closest. And for the next 6 minutes I am able to see it as bright as the sun moving away not getting any smaller visually. And it's now going to be over 1,250 miles. And I could see it the whole time. Do you see the contradiction of what you're telling me?
ChatGPT: I understand your point. The ISS appears bright because it's reflecting sunlight and it can be visible over a large portion of the sky. However, it does appear to get smaller and dimmer as it moves away from the observer's position.
DITRH: You told me just a few moments ago that if the if a 747 was directly and highly reflective sending sunlight to me at 50 mi away, I could not see it. Now, I've made— The ISS is five times farther when it's above me. It went an additional thousand miles away and I could see it the whole time. Can you explain to me how that is possible? You can't.
Dave made a few minor mistakes: for example, Bob pointed out that the “6 minutes” figure is the entire duration the ISS is visible from one horizon to the other, not from zenith to horizon. But Dave also made a few more serious mistakes, and created a vortex of ignorance that even sucked ChatGPT in.
See, ChatGPT is an LLM, which is fundamentally imitative and predictive with only an illusion of true comprehension. This means it has no innate awareness of truth, and its confidence when stating facts is a veneer. That's why at the bottom of ChatGPT.com it says “ChatGPT can make mistakes. Check important info.” But instead of calling them “mistakes,” AI engineers use a more candid technical term: hallucinations. The word “mistakes” implies relatable human limitations that are nonetheless governed by rational intelligence; in reality, AI chatbots are more like a vomiting electronic phychosis that's barely wrestled into a sometimes useful correlation with the facts in its training data.
This consumer ignorance about AI is a problem in general, but flat earthers like Dave Weiss take it to a whole new level. He approached ChatGPT as though it was an authority instead of a research assistant (which is already wrong), infected its responses with his own biases and naivete, and seemingly had no idea that he did so. This makes the conversation almost worthless for gleaning actual science info. When ChatGPT said you couldn't see a Boeing 747 at 50 miles away, it was simply wrong—or (generously speaking) it may have meant that a person wouldn't casually notice an airplane that far away, or that obscuring by clouds or mountains or refractive turbulence becomes very likely, etc. It obviously did not perform the kind of true quantitative analysis needed to cut through Dave's trap of confusion.
So how would a real scientist answer Dave's question: “Could I see a Boeing 747 50 miles away?” Well, for a brief, precarious moment Dave halfway acknowledged one of the variables in the scenario: object brightness. In saying this, Dave strayed mere inches from the door to a whole family of science concepts—then he ran from it like a conman from the cops. Let me open that door for you now.
Apparent Magnitude
If you have a sky object like a star—or a Boeing 747—there is a measurement used in astronomy for how visible it is, called apparent magnitude. After coordinates, magnitude is the next most important number used to catalogue and classify stars. Any time you look one up, you'll see it listed.
Now, magnitude can be a little confusing at first because it works backward. The brighter the star, the smaller the number. And on top of that, it's a dimensionless quantity that doesn't clearly tie back to the basic physics that we learn in high school, like Watts or Joules. Well, let's quickly build that bridge.
Light is radiant energy, and we know there are many frequencies beyond our visual perception. The most direct study of quantities of radiant energy is a field called radiometry, where “brightness” of an object actually is measured in units like Watts, as you might expect. But if we want brightness to the human eye, we have to exclude invisible frequencies—or technically, weight them according to a “luminosity function” that models the spectral response of a human retina. That's where you get units like lumens, which use a very specific model of the human retina that's standardized as ISO/CIE 23539:2023. In fact this creates a whole branch of radiometry called photometry. Since the physics are the same, the two fields often share equations; but in photometry, the variables are usually subscripted with a V to help distinguish.
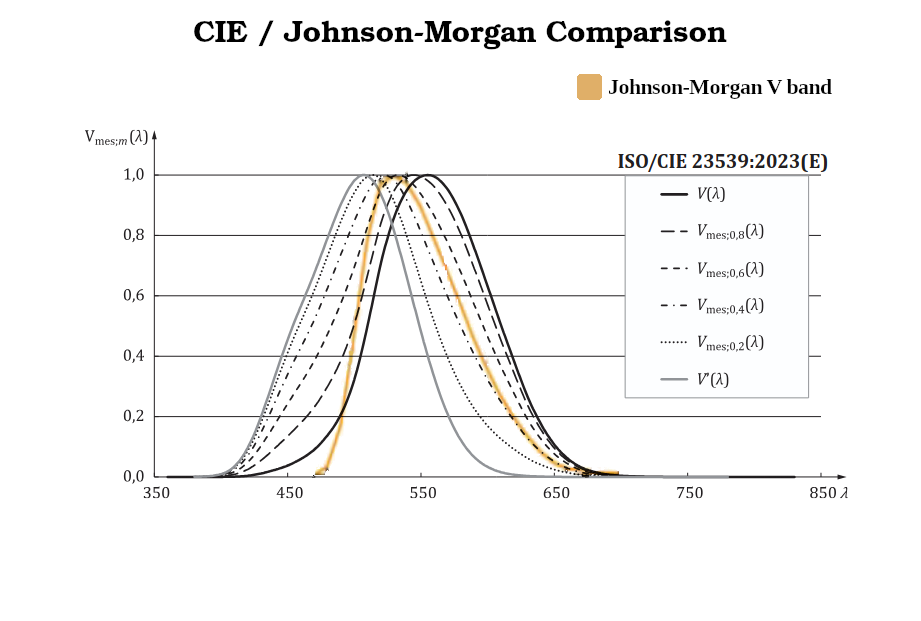
Now, a quick note about this standardized retina model. Other scientists in a different field unsurprisingly found a similar need to sometimes factor out invisible frequencies, so in astronomy you'll often see star measurements marked with different passband symbols like U, B, or V. Here, the formal standard is called the Johnson-Morgan system. The V stands for “visible;” it's very close (but not identical) to the aforementioned CIE standard, upon which the “lumen” unit is based. For purposes of this discussion we'll treat them as equal, but be aware that they are technically different.
The below plot overlays the relevant spectral response curves from the two standards, providing a visual comparison. The CIE spectral curve was taken from here; the Johnson-Morgan spectral curve was taken from here. The CIE defines multiple curves because of variations in retinal properties near the center (photopic) vs. toward the edge (scotopic), etc.
So, we finally arrive at a physical quantity (with a standardized unit) that correlates with star magnitude: it's called illuminance, or luminous flux density on a receiving surface like a retina or camera sensor. (The “luminous” part is to distinguish from general radiometry.) The units are lumens per square meter, or simply lux. Accounting for attenuation from the earth's atmosphere, it corresponds with magnitude like so:
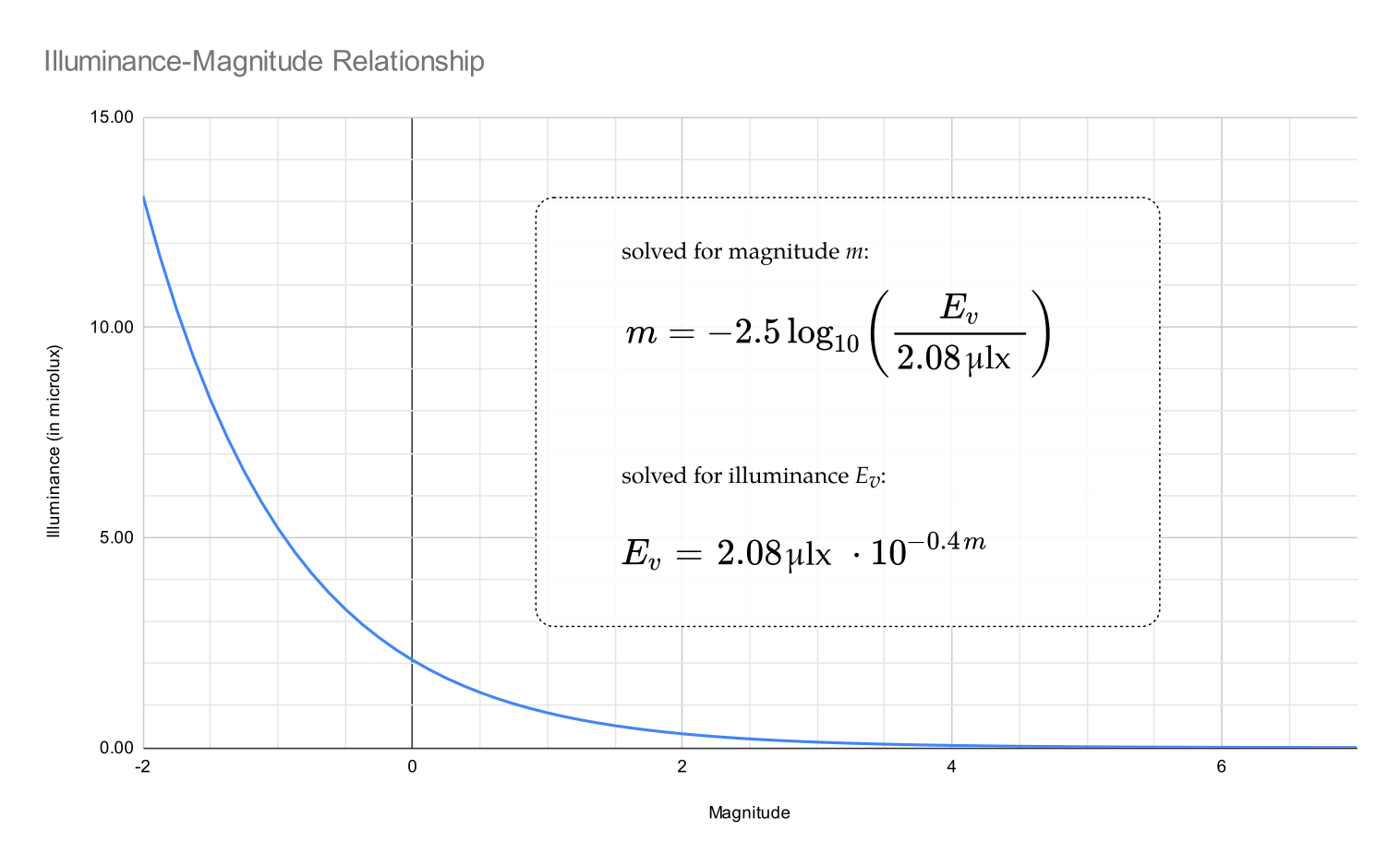
| Magnitude | Illuminance (in microlux) |
| -2.0 | 13.1239 |
| -1.5 | 8.2806 |
| -1.0 | 5.2247 |
| -0.5 | 3.2966 |
| 0.0 | 2.0800 |
| 0.5 | 1.3124 |
| 1.0 | 0.8281 |
| 1.5 | 0.5225 |
| 2.0 | 0.3297 |
| 2.5 | 0.2080 |
| 3.0 | 0.1312 |
| 3.5 | 0.0828 |
| 4.0 | 0.0522 |
| 4.5 | 0.0330 |
| 5.0 | 0.0208 |
| 5.5 | 0.0131 |
| 6.0 | 0.0083 |
| 6.5 | 0.0052 |
| 7.0 | 0.0033 |
The above “2.08 μlx” constant is according to the info at this source (2.54 μlx × 0.82 atmospheric dimming).
Magnitude from Luminance & Angular Size
Now if we move a luminous object farther from an observer, the observer will receive less light from it according to the inverse square law—a science concept which is among those most frequently butchered by flat earthers. Contrary to their belief, the observer will not receive less light due to the object's surface appearing to get dimmer. Rather, the inverse square law (as it's defined) is exclusively due to the object growing smaller in angular area to the observer's eye. This means the brightness of an object to an observer depends on both its angular size, and a distance-invariant property called luminance, measured in lux per square radian, or “nits.” Astronomers also sometimes measure luminance in magnitudes per square arcsecond, in which case it's called surface brightness.
So if we know an object's surface luminance and angular size, we can calculate its illuminance on the observer (and therefore its magnitude) like so:

where:
- EV = illuminance on the observer, in lux
- LV = surface luminance, in nits (lux per square radian)
- Ω = angular area of the object, in steradians (square radians)
This means we have all the ingredients for a process to quantify the visibility of sky objects and predict how a change of distance will affect perceived brightness. I gathered the requisite measurements and estimates for a range of objects in this spreadsheet, which I have plotted below. This includes:
- the navigational stars
- the sun, moon, and seven planets plus Pluto
- a lightbulb
- the ISS
- a Boeing 747 (just for DITRH 🥔)
The angular diameters of stars were mostly taken from the JMMC Stellar Diameter Catalog (JSDC) version 2 (using the Uniform-Disk value in the V passband). In 7 cases (Adhara, Avior, Dubhe, Acrux, Spica, Hadar, Sabik) the JMMC SearchCal tool was used instead; and in 2 cases (Menkar and Arcturus) this Wikipedia page was used. The planets' magnitudes and angular diameters were taken from Stellarium for August 20, 2025. For the ISS, Stellarium gave a maximum angular diameter of 48.02 arcseconds, which corresponds to the truss length of ~108 meters. A projected area portion was calculated from this for an effective uniform-disc diameter of 43.1 meters, or 19.2 arcseconds.
Since the human eye can see objects of magnitude +6 at night and -4 during the day, seeing a sunlit Boeing 747 at a distance of 50 miles (size of 82 arcseconds) would be no problem—if you knew exactly where in the sky to look. As we consider objects at greater and greater distances, long before it became actually invisible it would become a needle-in-a-haystack problem. That's why you typically need a tracker app or website in order to spot the ISS.
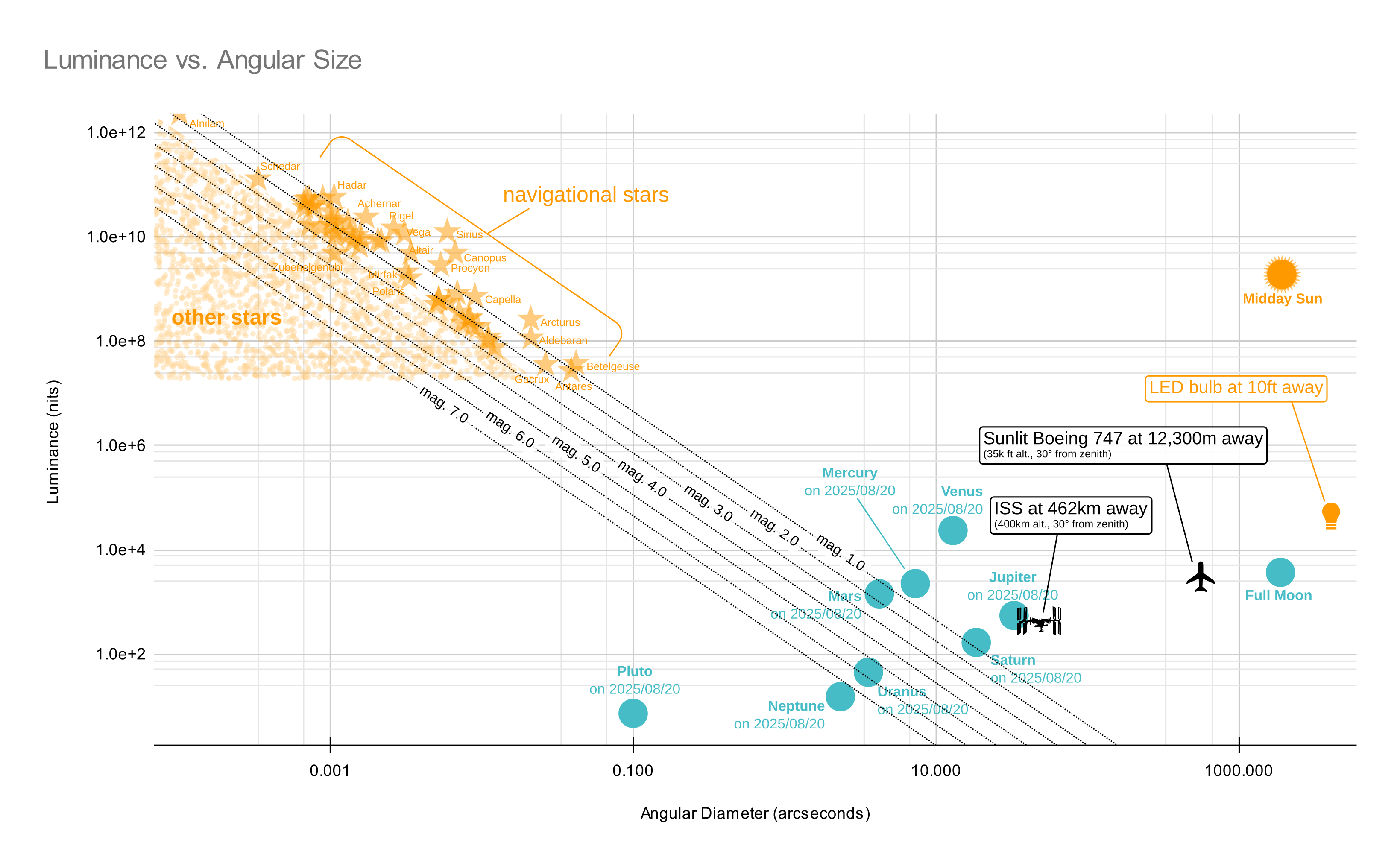
I have also contributed this chart to Wikimedia Commons.
